动手实验:利用矩形纸片(如图1)剪出一个正六边形纸片;再利用这个正六边形纸片做一个无盖的正六棱柱(棱柱底面为正六边形),如图2.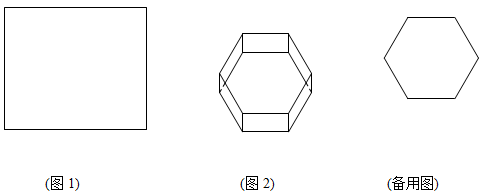
(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2)在(1)的条件下,当矩形的长为2a时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率为多少?(矩形纸片的利用率= .)
.)
相关知识点
推荐套卷
动手实验:利用矩形纸片(如图1)剪出一个正六边形纸片;再利用这个正六边形纸片做一个无盖的正六棱柱(棱柱底面为正六边形),如图2.
(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2)在(1)的条件下,当矩形的长为2a时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率为多少?(矩形纸片的利用率= .)
.)