如图，在△ABC中，∠ACB＝90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF＝CE．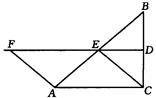
（1）求证：四边形ACEF是平行四边形；
（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论；
（3）四边形ACEF有可能是正方形吗？为什么？
相关试题
已知二次函数y=ax2+bx+2，它的图像经过点（1，2）．如果用含a的代数式表示b，那么b= ；
如图所示，如果该图像与x轴的一个交点为（－1，0）．
① 求二次函数的表达式，并写出图像的顶点坐标；
②在平面直角坐标系中，如果点P到x轴与y轴的距离相等，则称点P为等距点．求出这个二次函数图像上所有等距点的坐标．当a取a1,a2时，二次函数图像与x轴正半轴分别交于点M（m，0），点N（n，0）．如果点N在点M的右边，且点M和点N都在点（1，0）的右边．试比较a1和a2的大小．
如图，在△ABC中，AB=AC=10，BC=16，M为BC的中点．⊙A的半径为3，动点O从点B出发沿BC方向以每秒1个单位的速度向点C运动，设运动时间为t秒．当以OB为半径的⊙O与⊙A相切时，求t的值；
探究：在线段BC上是否存在点O，使得⊙O与直线AM相切，且与⊙A相外切．若存在，求出此时t的值及相应的⊙O的半径；若不存在，请说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号