如图,抛物线y=-x2+(m+2)x-3(m-1)交x轴于A、B,交y轴于C.直线y=(m+1)x-3经过点A.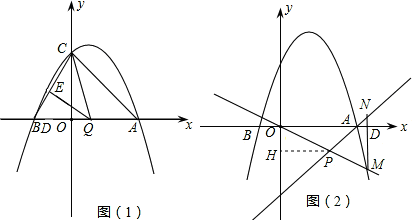
(1)求抛物线的解析式;
(2)点Q为线段AB上的动点,过点Q作QE∥AC,交BC于E,连CQ.当S△CQE的面积最大时,求点Q的坐标;
(3)直线y=kx(k<0)交直线y=(m+1)x-3于P,交抛物线y=-x2+(m+2)x-3(m-1)于点M,过M作x轴的垂线,垂足为D,交直线y=(m+1)x-3于N.△PMN能否为等腰三角形?若能,求k的值;若不能,说明理由.
相关知识点
推荐套卷
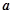 与
与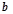 是否平行,并说明理由;
是否平行,并说明理由;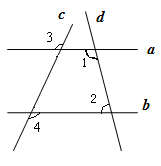
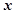 、
、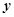 方程组
方程组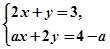 的解满足
的解满足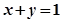 ,求
,求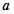 的值.
的值.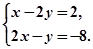
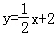 交y轴于点C,且过点D(8,m).
交y轴于点C,且过点D(8,m).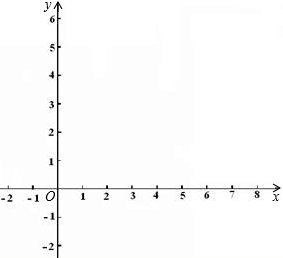
 粤公网安备 44130202000953号
粤公网安备 44130202000953号