某校部分男生分3组进行引体向上训练，对训练前后的成绩进行统计分析，相应数据的统计图如下．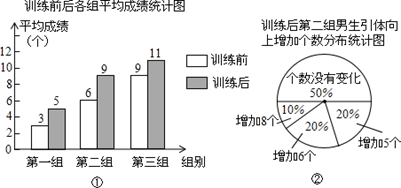
（1）求训练后第一组平均成绩比训练前增长的百分数；
（2）小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均成绩不可能提高3个这么多．”你同意小明的观点吗？请说明理由；
（3）你认为哪一组的训练效果最好？请提供一个解释来支持你的观点．
相关试题
如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线l，过点B作l的垂线BD，垂足为D，BD与⊙O交于点 E． 
(1). 求∠AEC的度数；
(2). 求证：四边形OBEC是菱形．
，并将其解集在数轴上表示出来. 
如图，
两点在函数
的图象上．
(1). 求
的值及直线
的解析式
(2). 如果一个点的横、纵坐标均为整数，那么我们称这个点是格点，请直接写出图中阴影部分（不包括边界）所含格点的个数．
，其中
．
相关知识点
推荐套卷
粤公网安备 44130202000953号