用同样规格的黑白两种颜色的正方形，按如图的方式拼图，请根据图中的信息完成下列问题．
（1）在图②中用了 块黑色正方形，在图③中用了 块黑色正方形；
（2）按如图的规律继续铺下去，那么第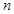
个图形要用 块黑色正方形；
（3）如果有足够多的白色正方形，能不能恰好用完90块黑色正方形，拼出具有以上规律的图形？
如果可以请说明它是第几个图形；如果不能，说明你的理由．
相关试题
用同样规格的黑白两种颜色的正方形，按如图的方式拼图，请根据图中的信息完成下列问题．
（1）在图②中用了 块黑色正方形，在图③中用了 块黑色正方形；
（2）按如图的规律继续铺下去，那么第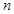个图形要用 块黑色正方形；
（3）如果有足够多的白色正方形，能不能恰好用完90块黑色正方形，拼出具有以上规律的图形？
如果可以请说明它是第几个图形；如果不能，说明你的理由．
；
；
；
.
中，
，
，一只蚂蚁从
点出发，沿长方体表面爬到
点，求蚂蚁怎样走最短，最短路程是多少？
，使点
落在
边上的点
处，
cm，
cm，
的长；（2）
的长.
的值.
粤公网安备 44130202000953号