如图,在平面直角坐标系中，△ABC是直角三角形,∠ACB=90,AC=BC,OA=1，OC=4，抛物线y=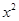
+bx+c经过A，B两点，抛物线的顶点为D．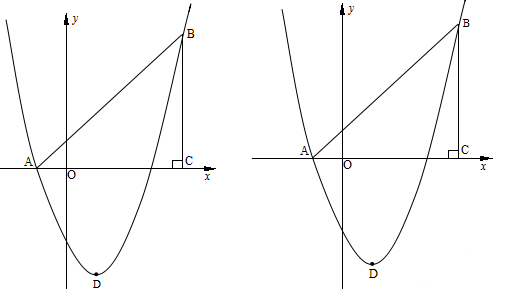
（1）求b,c的值；
（2）点E是直角三角形ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；
（3）在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形? 若存在，求出所有点P的坐标；若不存在，说明理由．
相关试题
的直径
的长为2
，
在
的延长线上，且
.
的度数；
是
，其中
是弧长，
是半径，
是圆心角度数）某校对中考前一次数学模拟考试进行抽样分析，把样本成绩按分数段分成
五组（每组成绩含最低分，不含最高分）进行统计，并将结果绘制成下面两幅统计图.
请根据图中信息，解答下列问题：
（1）求
组人数在扇形图中所占圆心角的度数；
（2）求
组人数；
（3）判断考试成绩的中位数落在哪个组？（直接写出结果，不需要说明理由）
是
对角线
上的两点，且
.
；
.
米，到对面较高楼房的距离
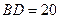米，当阳光刚好从两楼房的顶部射入时，测得光线与水平线的夹角为
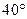.据此，小明便知楼房
的高度.请你写出计算过程
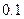米.参考数据：
）.相关知识点
推荐套卷
粤公网安备 44130202000953号