如图，小明家所住楼房的高度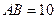
米，到对面较高楼房的距离
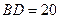米，当阳光刚好从两楼房的顶部射入时，测得光线与水平线的夹角为
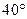.据此，小明便知楼房
的高度.请你写出计算过程
（结果精确到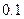
米.参考数据：
）.
的解是一对正数，则：
，并把解集在数轴上表示出来．
相关知识点
推荐套卷
如图，小明家所住楼房的高度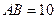米，到对面较高楼房的距离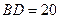米，当阳光刚好从两楼房的顶部射入时，测得光线与水平线的夹角为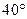.据此，小明便知楼房的高度.请你写出计算过程
（结果精确到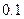米.参考数据：）.
粤公网安备 44130202000953号