在平面直角坐标系xOy中,直线 分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线
分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线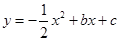 经过A,C两点,与
经过A,C两点,与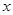 轴的另一交点为D.
轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线AB与CD的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,B,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
在平面直角坐标系xOy中,直线 分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线
分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线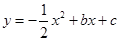 经过A,C两点,与
经过A,C两点,与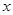 轴的另一交点为D.
轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线AB与CD的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,B,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.