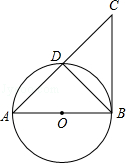
(本小题满分14分)如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD,AC为对角线,BD=8.
①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在, 请说明理由;
②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE.当四边形ABED为菱形时,求点F到AB 的距离.
相关知识点
推荐套卷
 ,其中x=3.
,其中x=3.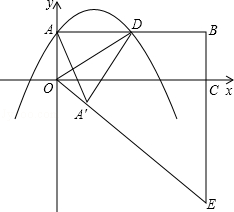

 ,BP′=
,BP′=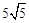 时,求线段AB的长.
时,求线段AB的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号