如图①所示，在正方形ABCD中，M是AB的中点，E是AB的延长线上一点，MN⊥DM，且交∠CBE的平分线于点N．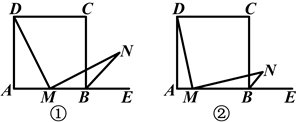
(1)求证：MD＝MN；
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”，其余条件不变，如图②所示，则结论“MD＝MN”还成立吗？若成立，给出证明；若不成立，请说明理由．
如图①所示，在正方形ABCD中，M是AB的中点，E是AB的延长线上一点，MN⊥DM，且交∠CBE的平分线于点N．
(1)求证：MD＝MN；
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”，其余条件不变，如图②所示，则结论“MD＝MN”还成立吗？若成立，给出证明；若不成立，请说明理由．
粤公网安备 44130202000953号