(本小题满分1 2分)如图,梯形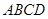 中,
中,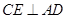 于
于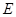 ,
, 于
于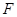 ,且
,且
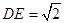 ,现将
,现将 ,
, 分别沿
分别沿 与
与 翻折,使点
翻折,使点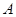 与点
与点 重合.
重合.
(1)设面 与面
与面 相交于直线
相交于直线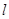 ,求证:
,求证: ;
;
(2)试类比求解三角形的内切圆(与三角形各边都相切)半径的方法,求出四棱锥 的内切球(与四棱锥各个面都相切)的半径.
的内切球(与四棱锥各个面都相切)的半径.
相关知识点
推荐套卷
(本小题满分1 2分)如图,梯形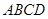 中,
中,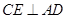 于
于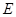 ,
, 于
于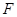 ,且
,且
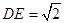 ,现将
,现将 ,
, 分别沿
分别沿 与
与 翻折,使点
翻折,使点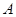 与点
与点 重合.
重合.
(1)设面 与面
与面 相交于直线
相交于直线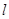 ,求证:
,求证: ;
;
(2)试类比求解三角形的内切圆(与三角形各边都相切)半径的方法,求出四棱锥 的内切球(与四棱锥各个面都相切)的半径.
的内切球(与四棱锥各个面都相切)的半径.