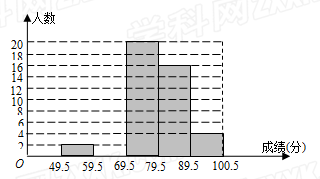
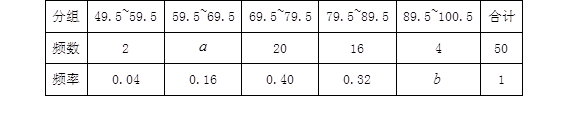某班体育委员小华对本班近期体育测验成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数、频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
(1)频数、频率分布表中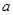 = ,
= ,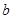 = ;
= ;
(2)补全频数分布直方图;
(3)班主任准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是多少?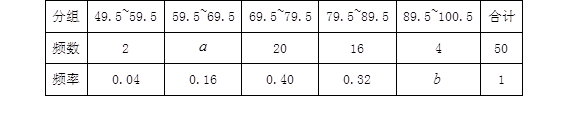
相关知识点
推荐套卷
某班体育委员小华对本班近期体育测验成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数、频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
(1)频数、频率分布表中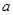 = ,
= ,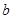 = ;
= ;
(2)补全频数分布直方图;
(3)班主任准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是多少?