为了分流地铁高峰的压力,某市发改委通过听众会,决定实施低峰优惠票价制度.不超过 公里的地铁票价如下表:
公里的地铁票价如下表:
乘坐里程 (单位: (单位: ) ) |
 |
 |
 |
| 票价(单位:元) |
 |
 |
 |
现有甲、乙两位乘客,他们乘坐的里程都不超过 公里.已知甲、乙乘车不超过
公里.已知甲、乙乘车不超过 公里的概率分别为
公里的概率分别为 ,
, ,甲、乙乘车超过
,甲、乙乘车超过 公里且不超过
公里且不超过 公里的概率分别为
公里的概率分别为 ,
, .
.
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
相关知识点
推荐套卷
 x-y
x-y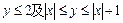 围成的几何图形的面积是多少?
围成的几何图形的面积是多少? 产品
产品 粤公网安备 44130202000953号
粤公网安备 44130202000953号