若
是一个三位正整数,且
的个位数字大于十位数字,十位数字大于百位数字,则称
为"三位递增数"(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的"三位递增数"中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的"三位递增数"的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(Ⅰ)写出所有个位数字是5的"三位递增数" ;
(Ⅱ)若甲参加活动,求甲得分
的分布列和数学期望
.
相关知识点
推荐套卷
 的上顶点为
的上顶点为 ,右焦点为
,右焦点为 ,直线
,直线 与圆
与圆
 相切.
相切. 的方程;
的方程; 与椭圆
与椭圆 、
、 两点,且
两点,且 求证:直线
求证:直线 的坐标.
的坐标.
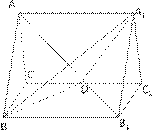
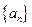 中,
中,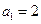 ,
, ,
,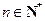 .
.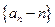 是等比数列;
是等比数列;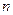 项和
项和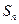 ,求
,求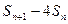 的最大值
的最大值 ,在函数
,在函数 的图象中,对称中心到对称轴的最小距离为
的图象中,对称中心到对称轴的最小距离为 且当
且当 的最大值为1。
的最大值为1。 的解析式;
的解析式; 的不等式
的不等式
 粤公网安备 44130202000953号
粤公网安备 44130202000953号