（本小题满分12分）节能减排是现代生活的追求。长沙地区某一天的温度（单位：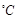
）随时间
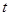（单位：小时）的变化近似满足函数关系：
，
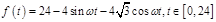且早上8时的温度为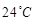
，
．
（Ⅰ）求函数的解析式，并判断这一天的最高温度是多少？出现在何时？
（Ⅱ）某通宵营业的超市，为节约能源和开支，在环境温度超过
时，才开启中央空调降温，否则关闭中央空调，问中央空调应在何时开启？何时关闭？
，是否存在整式
，使得
对n≥2的一切自然数都成立?并试用数学
的展开式中，第6项与第7的系数相等,求展开式中二项式系数最大的项和系数最大的项．
求证:
推荐套卷
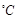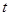（本小题满分12分）节能减排是现代生活的追求。长沙地区某一天的温度（单位：）随时间（单位：小时）的变化近似满足函数关系：，
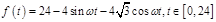且早上8时的温度为，．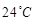
（Ⅰ）求函数的解析式，并判断这一天的最高温度是多少？出现在何时？
（Ⅱ）某通宵营业的超市，为节约能源和开支，在环境温度超过时，才开启中央空调降温，否则关闭中央空调，问中央空调应在何时开启？何时关闭？
粤公网安备 44130202000953号