(本小题满分12分)如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为[50,60),[60,70),[70,80),[80,90),[90,100],据此解答如下问题.

(1)求全班人数及分数在[80,100]之间的频率;
(2)现从分数在[80,100]之间的试卷中任取 份分析学生失分情况,设抽取的试卷分数在[90,100]的份数为 X ,求 X 的分布列和数学望期.
份分析学生失分情况,设抽取的试卷分数在[90,100]的份数为 X ,求 X 的分布列和数学望期.
相关知识点
推荐套卷

 (t为参数),直线l与曲线C相交于A、B两点求|AB|的值
(t为参数),直线l与曲线C相交于A、B两点求|AB|的值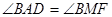 :
: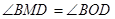 .
.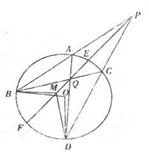
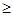 x2在(0,1 )上恒成立,求实数a的取值范围.
x2在(0,1 )上恒成立,求实数a的取值范围.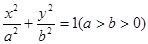 的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.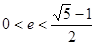 ,0为坐标原点,求证
,0为坐标原点,求证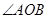 为钝角.
为钝角.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号