（本题10分）在平面直角坐标系
中，对于任意三点
、
、
的“矩面积”，给出如下定义：“水平底”
：任意两点横坐标差的最大值，“铅垂高”
：任意两点纵坐标差的最大值，则“矩面积”
．
例如：三点坐标分别为
，
，
，则“水平底”
，“铅垂高”
，“矩面积”
．
（1）已知点
，，
．
①若、、
三点的“矩面积”为
，求点的坐标；
②、、三点的“矩面积”的最小值为 ．
（2）已知点
，
，
，其中
．若
、
、
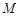三点的“矩面积”的为
，求
的取值范围；
相关试题
＝0，化简代数式后求值：
如图是某城市出租车单程收费Y（元）与行驶路程X（千米）之间的函数关系图像，根据图像回答下列问题：
（1）从图像上你能得到哪些信息？（请写出2条）
（2）求出收费Y（元）与行驶路程X（千米）（X≥3）之间的函数关系式。
●
●
的图像经过点（－2，4）且与直线
平行，求这个一次函数的解析式。相关知识点
推荐套卷
粤公网安备 44130202000953号