如图，正方形ABCD中，CD＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．
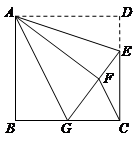
（1）求证：①△ABG≌△AFG； ②求GC的长；
（2）求△FGC的面积．
，其中
。
推荐套卷
如图，正方形ABCD中，CD＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．
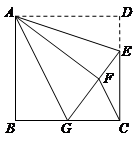
（1）求证：①△ABG≌△AFG； ②求GC的长；
（2）求△FGC的面积．
粤公网安备 44130202000953号