二次函数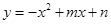
的图象经过点A（﹣1，4），B（1，0），
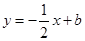经过点B，且与二次函数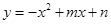交于点D．过点D作DC⊥x轴，垂足为点C．
（1）求二次函数的表达式；
（2）点N是二次函数图象上一点（点N在BD上方），过N作NP⊥x轴，垂足为点P，交BD于点M，求MN的最大值．
×（－8）；
×(8－1
－0.04)；
－
+
－
)×36；
×2.4×
；相关知识点
推荐套卷
二次函数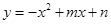的图象经过点A（﹣1，4），B（1，0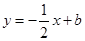），经过点B，且与二次函数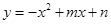交于点D．过点D作DC⊥x轴，垂足为点C．
（1）求二次函数的表达式；
（2）点N是二次函数图象上一点（点N在BD上方），过N作NP⊥x轴，垂足为点P，交BD于点M，求MN的最大值．
粤公网安备 44130202000953号