阅读下面的材料:
小敏在数学课外小组活动中遇到这样一个问题:
如果α,β都为锐角,且 ,
, ,求
,求 的度数.
的度数.
小敏是这样解决问题的:如图1,把 ,
, 放在正方形网格中,使得
放在正方形网格中,使得 ,
, ,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得
,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得 ="∠ABC" =
="∠ABC" =
°.
请参考小敏思考问题的方法解决问题:
如果 ,
, 都为锐角,当
都为锐角,当 ,
, 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=
时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON= ,由此可得
,由此可得 =______°.
=______°.
相关知识点
推荐套卷
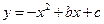 过点C(3,8),与
过点C(3,8),与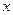 轴交于A,B两点,与y轴交于点D(0,5).
轴交于A,B两点,与y轴交于点D(0,5).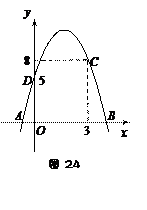
 气球与高楼的水平距离为60 m,这栋高楼有多高?(结果精确到0. 1 m,参考数据:sin50°≈0.78,cos50°≈0.
气球与高楼的水平距离为60 m,这栋高楼有多高?(结果精确到0. 1 m,参考数据:sin50°≈0.78,cos50°≈0. 64 ,tan50°≈1.19 ,
64 ,tan50°≈1.19 , ≈1.73 )
≈1.73 )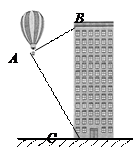

 DFE;
DFE;
 ),根据调查结果绘制了两幅尚不完整的统计图:
),根据调查结果绘制了两幅尚不完整的统计图:
 所提供的信息,完
所提供的信息,完 粤公网安备 44130202000953号
粤公网安备 44130202000953号