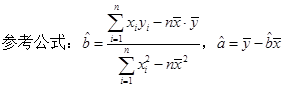（本小题满分12分）
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作四次试验，得到的数据如下：
| 零件的个数x（个） |
2 |
3 |
4 |
5 |
| 加工的时间y（小时） |
2．5 |
3 |
4 |
4．5 |
（1）已知零件个数与加工时间线性相关，求出y关于x的线性回归方程；
（2）试预测加工10个零件需要多少时间？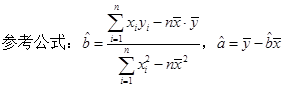
是等差数列，且
.
，求数列
的前
项和．
中，角
的对边分别为
且
.
;
，求
的前
项和
,又
，求数列
的前
.
中，
分别为角
的对边，
.
的度数；
,求
与
的值.
为等差数列，且
.
项和为
，若
成等比数列，求正整数
的值.推荐套卷
（本小题满分12分）
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作四次试验，得到的数据如下：
| 零件的个数x（个） |
2 |
3 |
4 |
5 |
| 加工的时间y（小时） |
2．5 |
3 |
4 |
4．5 |
（1）已知零件个数与加工时间线性相关，求出y关于x的线性回归方程；
（2）试预测加工10个零件需要多少时间？
粤公网安备 44130202000953号