(本小题满分14分)
在平面直角坐标系xoy中,椭圆C :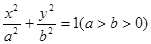 的离心率为
的离心率为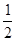 ,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:
,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O: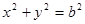 相切于点M.
相切于点M.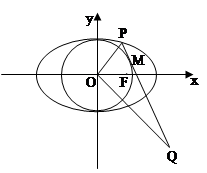
(1)求椭圆C的方程;
(2)求|PM|·|PF|的取值范围;
(3)若OP⊥OQ,求点Q的纵坐标t的值.
推荐套卷
(本小题满分14分)
在平面直角坐标系xoy中,椭圆C :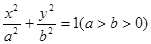 的离心率为
的离心率为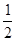 ,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:
,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O: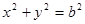 相切于点M.
相切于点M.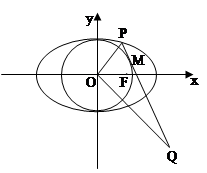
(1)求椭圆C的方程;
(2)求|PM|·|PF|的取值范围;
(3)若OP⊥OQ,求点Q的纵坐标t的值.