李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题，请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长．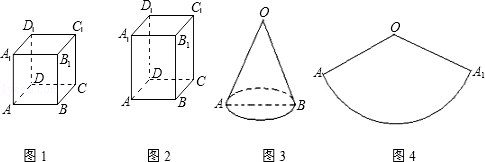
（1）如图1，正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处；
（2）如图2，正四棱柱的底面边长为5cm，侧棱长为6cm，一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处；
（3）如图3，圆锥的母线长为4cm，圆锥的侧面展开图如图4所示，且∠AOA1=120°，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A．
相关试题
三个同学对问题：“若方程组
的解是
求方程组
的解”提出了各自的想法．甲说：“这个题目好像条件不够，不能求解．”乙说：“它们的系数有一定的规律，可以试试．”丙说：“能不能把第二个方程组中两个方程的两边都除以5，通过换元的方法来解决．”参考他们的讨论，你认为这个题目的解是．
相关知识点
推荐套卷
粤公网安备 44130202000953号