二次函数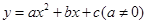
的图象与
轴交于A（－3，0）、B（1，0）两点，与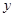
轴交于点C（0，
）（其中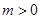
），顶点为D．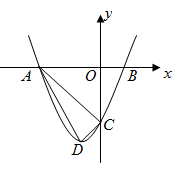
（1）用含
的代数式分别表示
、
、
；
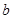（2）如图，当取何值时，△ADC为直角三角形？
，求这个多边形的边数．相关知识点
推荐套卷
二次函数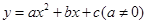的图象与轴交于A（－3，0）、B（1，0）两点，与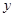轴交于点C（0，）（其中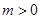），顶点为D．
（1）用含的代数式分别表示、、；
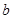（2）如图，当取何值时，△ADC为直角三角形？
粤公网安备 44130202000953号