如图：在直角坐标系中，以点A（3，0）为圆心，以5为半径的圆与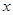
轴相交于B、C两点，与
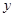轴相交于D、E两点.
若抛物线
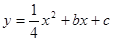经过C、D两点，求此抛物线的解析式，并判断点B是否在这条抛物线上？
过点E的直线
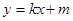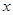交轴于F（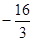
，0），求此直线的解析式，这条直线是⊙A的切线吗？请说明理由；
探索：是否能在（1）中的抛物线上找到一点Q，使直线BQ与
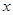轴正方向所夹锐角的正切值等于
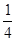？，若能，请直接写出Q点坐标；若不能，请说明理由. (4分)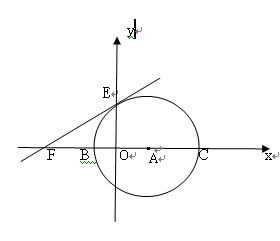
相关试题
设函数
（k是常数）．
（1）当k=1和k=2时的函数
和
的图像如图所示，请你在同一坐标系中画出k=3时函数
的图像；
（2）根据图像，写出你发现的两条结论；
（3）将函数
的图像向左平移2个单位，再向下平移4个单位，得到函数
的图像。请写出函数的解析式，回答自变量x取何值时，函数的最小值是多少？
的中点，CE⊥AB于点E，BD交CE于点F．
学校组织春游，安排九年级三辆车，小明与小慧都可以从这三辆车中任意选一辆搭乘。
（1）用树状图（或列表法）表示小明与小慧乘车所有可能出现的结果`（三辆车分别用甲、乙、丙表示）；
（2）求小明与小慧乘车不同的概率有多大？
相关知识点
推荐套卷
粤公网安备 44130202000953号