如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时, 当A,B,M,N在同一直线上时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.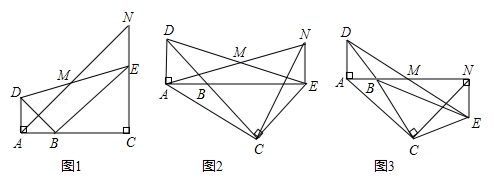
相关知识点
推荐套卷
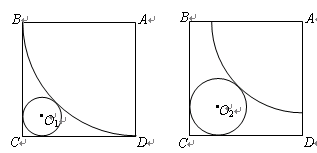
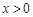 ),四边形BCDP的面积为y cm2.
),四边形BCDP的面积为y cm2.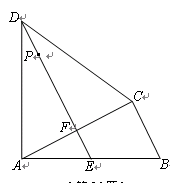
 解答下列问题:
解答下列问题: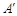 ,A与
,A与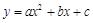 上,且这条抛物线与
上,且这条抛物线与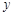 轴的交点的纵坐标为-6,求这条抛物线的顶点坐标.
轴的交点的纵坐标为-6,求这条抛物线的顶点坐标. 粤公网安备 44130202000953号
粤公网安备 44130202000953号