如图，抛物线与y轴相交于点A（0,2），与x轴相交于B（4,0）
C（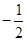
，0）两点.直线l经过A、B两点.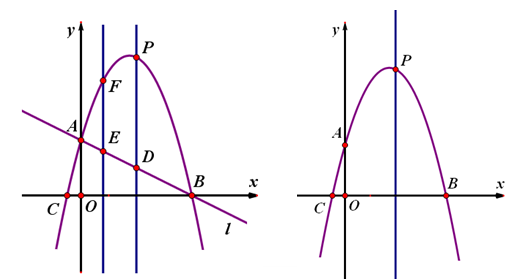
（1）分别求出直线l和抛物线相应的函数表达式；
（2）平行于y轴的直线x=2交抛物线于点P，交直线l于点D.① 直线x=t（0≤t≤4）与直线l相交于点E，与抛物线相交于点F.若EF：DP=3：4， 求t的值；② 将抛物线沿y轴上下平移，所得的抛物线与y轴交于点A′,与直线x=2交于点P′.当P′O平分∠A′P′P时，求平移后的抛物线相应的函数表达式.
相关试题
如图，已知，EG∥AF，请你从下面三个条件中，再选出两个作为已知条件，另一个作为结论，推出一个正确的命题。并证明这个命题（只写出一种情况）①AB="AC" ②DE="DF" ③BE=CF
已知：EG∥AF,_______,_________.
求证：___________.
证明:
相关知识点
推荐套卷
粤公网安备 44130202000953号