（本小题满分12分）在直角坐标系xOy中，以坐标原点O为圆心的圆与直线：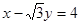
相切．
（Ⅰ）求圆O的方程；
（Ⅱ）圆O与x轴相交于A、B两点，圆内的动点P使|PA|、|PO|、|PB|成等比数列，求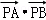
的取值范围．
相关试题
的性质，并在此基础上，作出其在
的图象
上的函数
的周期为
，且对一切
，都有
的表达式
中，
分别是角A，B，C的对边，已知
，
，△
，求
的值
，
，
，求
的值.
：
与抛物线C：
相切于点A
的值；（2）求以点A为圆心，且与抛物线C的准线相切的圆的方程 
的值；（2）若
为钝角，求实数相关知识点
推荐套卷
（本小题满分12分）在直角坐标系xOy中，以坐标原点O为圆心的圆与直线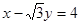：相切．
（Ⅰ）求圆O的方程；
（Ⅱ）圆O与x轴相交于A、B两点，圆内的动点P使|PA|、|PO|、|PB|成等比数列，求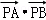的取值范围．
粤公网安备 44130202000953号