如图,正方形AOCB在平面直角坐标系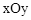 中,点O为原点,点B在反比例函数
中,点O为原点,点B在反比例函数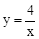 (
(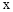 >
> )图象上, OB=
)图象上, OB=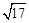 (OC>OA).
(OC>OA).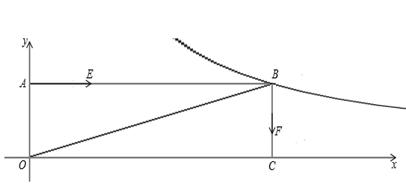
(1)求点B的坐标;
(2)若动点E从A开始沿AB向B以每秒2个单位的速度运动,同时动点F 从B开始沿BC向C以每秒1个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.当运动时间为 秒时,在x轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在x轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
如图,正方形AOCB在平面直角坐标系 中,点O为原点,点B在反比例函数
中,点O为原点,点B在反比例函数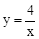 (
(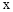 >
> )图象上, OB=
)图象上, OB=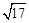 (OC>OA).
(OC>OA).
(1)求点B的坐标;
(2)若动点E从A开始沿AB向B以每秒2个单位的速度运动,同时动点F 从B开始沿BC向C以每秒1个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.当运动时间为 秒时,在x轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在x轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.