如图，在半径为2的扇形AOB中，∠AOB=60°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．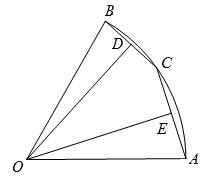
（1）当BC=1时，求线段OD的长；
（2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；
（3）设BD=x，△DOE的面积为y，求y关于x的函数关系式，并写出它的定义域。
如图，在边长为1个单位长度的小正方形组成的两格中，点A、B、C都是格点．
（1）将△ABC绕点C顺时针旋转
得到△A1B1C1；
（2）作△ABC关于点O成中心对称的△A2B2C2.
，其中
．问题情境：如图1，直角三角板ABC中，∠C＝90°，AC＝BC，将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上，再将该直角绕点D旋转，并使其两边分别与三角板的AC边、BC边交于P、Q两点。
问题探究：（1）在旋转过程中，
①如图2，当AD＝BD时，线段DP、DQ有何数量关系？并说明理由。
②如图3，当AD＝2BD时，线段DP、DQ有何数量关系？并说明理由。
③根据你对①、②的探究结果，试写出当AD＝nBD时，DP、DQ满足的数量关系为_______________（直接写出结论，不必证明）
（2）当AD＝BD时，若AB＝20，连接PQ，设△DPQ的面积为S，在旋转过程中，S是否存在最小值或最大值？若存在，求出最小值或最大值；若不存在，请说明理由。
图1 图2 图3
已知抛物线
与x轴交于点
、C，与y轴交于点B（0，3），抛物线的顶点为p。
（1）求抛物线的解析式；
（2）若抛物线向下平移k个单位后经过点（－5，6）。
①求k的值及平移后抛物线所对应函数的最小值；
②设平移后抛物线与y轴交于点D，顶点为Q，点M是平移后的抛物线上的一个动点。请探究：当点M在何处时，△MBD的而积是△MPQ面积的2倍？求出此时点M的坐标。
粤公网安备 44130202000953号