如图所示,过点F(0,1)的直线y=kx+b与抛物线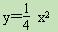 交于M(x1,
交于M(x1,
y1)和N(x2,y2)两点(其中x1<0,x2<0) .
.
(1)求b的值.
(2)求x1•x2的值
(3)分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判 断△M1FN1的形状,
断△M1FN1的形状,
并证明你的结论.
(4)对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相
切.如果有,请求出这条直线m的解析式;如果没有,请说明理由.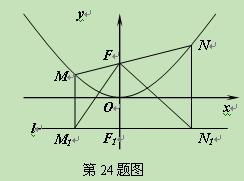
相关知识点
推荐套卷
如图所示,过点F(0,1)的直线y=kx+b与抛物线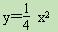 交于M(x1,
交于M(x1,
y1)和N(x2,y2)两点(其中x1<0,x2<0) .
.
(1)求b的值.
(2)求x1•x2的值
(3)分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判 断△M1FN1的形状,
断△M1FN1的形状,
并证明你的结论.
(4)对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相
切.如果有,请求出这条直线m的解析式;如果没有,请说明理由.