如图,对称轴为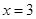 的抛物线
的抛物线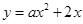 与
与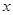 轴相交于点
轴相交于点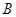 、
、 。
。
(1)求抛物线的解析式,并求出顶点 的坐标
的坐标
(2)连结AB,把AB所在的直线平移,使它经过原点O,得到直线 .点P是
.点P是 上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为
上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为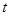 ,当0<S≤18时,求
,当0<S≤18时,求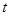 的取值范围
的取值范围
(3)在(2)的条件下,当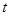 取最大值时,抛物线上是否存在点
取最大值时,抛物线上是否存在点 ,使△OP
,使△OP 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,对称轴为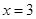 的抛物线
的抛物线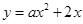 与
与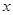 轴相交于点
轴相交于点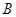 、
、 。
。
(1)求抛物线的解析式,并求出顶点 的坐标
的坐标
(2)连结AB,把AB所在的直线平移,使它经过原点O,得到直线 .点P是
.点P是 上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为
上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为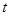 ,当0<S≤18时,求
,当0<S≤18时,求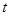 的取值范围
的取值范围
(3)在(2)的条件下,当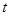 取最大值时,抛物线上是否存在点
取最大值时,抛物线上是否存在点 ,使△OP
,使△OP 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.