如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线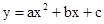
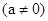 过点B。
过点B。
(1)若a=-l,且抛物线与矩形有且只有三个交点B、D、E,求△ BDE的面积S的最大值;
(2)若抛物线与矩形有且只有三个交点B、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线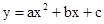
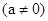 过点B。
过点B。
(1)若a=-l,且抛物线与矩形有且只有三个交点B、D、E,求△ BDE的面积S的最大值;
(2)若抛物线与矩形有且只有三个交点B、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。