如图，在四棱锥P—ABCD中，PA⊥AD，AB∥CD，CD⊥AD，AD =" CD" =" 2AB" = 2，E为PC的中点，DE = EC
（1）求证：
平面
（2）设PA = a，若平面EBD与平面ABCD所成锐二面角的为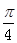
，求a的值。
，x∈R }，若A∩B = Æ，试求实数a的取值范围．
．
取最值时的
的值；
，求下列各式的值：
；
．
．
(7分)推荐套卷
如图，在四棱锥P—ABCD中，PA⊥AD，AB∥CD，CD⊥AD，AD =" CD" =" 2AB" = 2，E为PC的中点，DE = EC
（1）求证：平面
（2）设PA = a，若平面EBD与平面ABCD所成锐二面角的为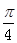，求a的值。
粤公网安备 44130202000953号