(年湖北天门学业12分)如图,已知二次函数的图象过点A(0,﹣3),B(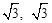 ),对称轴为直线
),对称轴为直线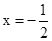 ,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=
,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC= MP,MD=
MP,MD= OM,OE=
OM,OE= ON,NF=
ON,NF= NP.
NP.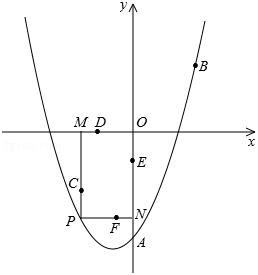
(1)求此二次函数的解析式;
(2)求证:以C、D、E、F为顶点的四边形CDEF是平行四边形;
(3)在抛物线上是否存在这样的点P,使四边形CDEF为矩形?若存在,请求出所有符合条件的P点坐标;若不存在,请说明理由.
(年湖北天门学业12分)如图,已知二次函数的图象过点A(0,﹣3),B(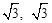 ),对称轴为直线
),对称轴为直线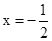 ,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=
,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC= MP,MD=
MP,MD= OM,OE=
OM,OE= ON,NF=
ON,NF= NP.
NP.
(1)求此二次函数的解析式;
(2)求证:以C、D、E、F为顶点的四边形CDEF是平行四边形;
(3)在抛物线上是否存在这样的点P,使四边形CDEF为矩形?若存在,请求出所有符合条件的P点坐标;若不存在,请说明理由.