（年山东德州12分）如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．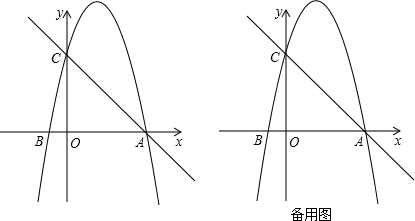
（1）求抛物线的解析式；
（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直于y轴于点E，交直线AC于点D，过点D作y轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．
如图所示，在平面直角坐标系中，Rt△OBC的两条直角边分别落在x轴、y轴上，且OB=1,OC=3,将△OBC绕原点O顺时针旋转90°得到△OAE，将△OBC沿y轴翻折得到△ODC，AE与CD交于点F.
（1）若抛物线过点A、B、C, 求此抛物线的解析式;
（2）求△OAE与△ODC重叠的部分四边形ODFE的面积;
（3）点M是第三象限内抛物线上的一动点，点M在何处时△AMC的面积最大？最大面积是多少？求出此时点
的坐标.
如图，矩形ABCD中，AB=16cm，AD=4cm，点P、Q分别从A、B同时出发，点P在边AB上沿AB方向以2cm/s的速度匀速运动，点Q在边BC上沿BC方向以1cm/s的速度匀速运动，当其中一点到达终点时，另一点也随之停止运动.设运动时间为x秒，△PBQ的面积为y（cm2）.
（1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的最大值.
已知：如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点P，PD⊥AC于点D．
（1）求证：PD是⊙O的切线；
（2）若∠CAB=120°，AB=6，求BC的值．
如图，抛物线y=－x2+（m－1）x+m与y轴交于（0，3）点，
（1）求出这条抛物线；
（2）求它与x轴的交点和抛物线顶点的坐标；
（3）x取什么值时，抛物线在x轴上方?
（4）x取什么值时，y的值随x的增大而减小？
粤公网安备 44130202000953号