如图,平面直角坐标系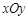 中,已知点
中,已知点 (2,3),线段
(2,3),线段 垂直于
垂直于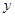 轴,垂足为
轴,垂足为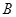 ,将线段
,将线段 绕点A逆时针方向旋转
绕点A逆时针方向旋转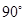 ,点
,点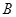 落在点
落在点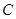 处,直线
处,直线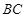 与
与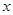 轴的交于点
轴的交于点 .
.
(1)试求出点 的坐标;
的坐标;
(2)试求经过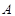 、
、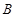 、
、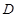 三点的抛物线的表达式,并写出其顶点E的坐标;
三点的抛物线的表达式,并写出其顶点E的坐标;
(3)在(2)中所求抛物线的对称轴上找点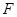 ,使得以点
,使得以点 、
、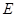 、
、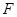 为顶点的三角形与△
为顶点的三角形与△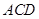 相似.
相似.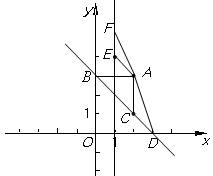
相关知识点
推荐套卷
如图,平面直角坐标系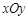 中,已知点
中,已知点 (2,3),线段
(2,3),线段 垂直于
垂直于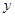 轴,垂足为
轴,垂足为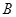 ,将线段
,将线段 绕点A逆时针方向旋转
绕点A逆时针方向旋转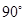 ,点
,点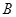 落在点
落在点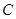 处,直线
处,直线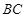 与
与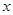 轴的交于点
轴的交于点 .
.
(1)试求出点 的坐标;
的坐标;
(2)试求经过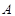 、
、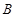 、
、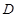 三点的抛物线的表达式,并写出其顶点E的坐标;
三点的抛物线的表达式,并写出其顶点E的坐标;
(3)在(2)中所求抛物线的对称轴上找点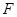 ,使得以点
,使得以点 、
、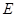 、
、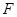 为顶点的三角形与△
为顶点的三角形与△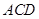 相似.
相似.