(年辽宁丹东14分)如图1,抛物线y=ax2+bx﹣1经过A(﹣1,0)、B(2,0)两点,交y轴于点C.点P为抛物线上的一个动点,过点P作x轴的垂线交直线BC于点D,交x轴于点E.
(1)请直接写出抛物线表达式和直线BC的表达式.
(2)如图1,当点P的横坐标为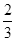 时,求证:△OBD∽△ABC.
时,求证:△OBD∽△ABC.
(3)如图2,若点P在第四象限内,当OE=2PE时,求△POD的面积.
(4)当以点O、C、D为顶点的三角形是等腰三角形时,请直接写出动点P的坐标.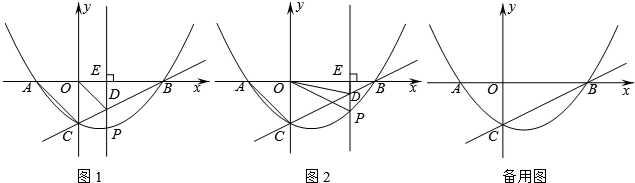
(年辽宁丹东14分)如图1,抛物线y=ax2+bx﹣1经过A(﹣1,0)、B(2,0)两点,交y轴于点C.点P为抛物线上的一个动点,过点P作x轴的垂线交直线BC于点D,交x轴于点E.
(1)请直接写出抛物线表达式和直线BC的表达式.
(2)如图1,当点P的横坐标为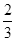 时,求证:△OBD∽△ABC.
时,求证:△OBD∽△ABC.
(3)如图2,若点P在第四象限内,当OE=2PE时,求△POD的面积.
(4)当以点O、C、D为顶点的三角形是等腰三角形时,请直接写出动点P的坐标.