（年湖北江汉油田、潜江、天门、仙桃12分）已知抛物线经过A（﹣2，0），B（0，2），C（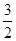
，0）三点，一动点P从原点出发以1个单位/秒的速度沿x轴正方向运动，连接BP，过点A作直线BP的垂线交y轴于点Q．设点P的运动时间为t秒．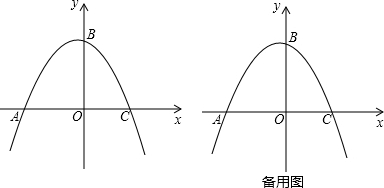
（1）求抛物线的解析式；
（2）当BQ=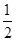
AP时，求t的值；
（3）随着点P的运动，抛物线上是否存在一点M，使△MPQ为等边三角形？若存在，请直接写t的值及相应点M的坐标；若不存在，请说明理由．
相关试题
（年湖北江汉油田、潜江、天门、仙桃12分）已知抛物线经过A（﹣2，0），B（0，2），C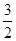（，0）三点，一动点P从原点出发以1个单位/秒的速度沿x轴正方向运动，连接BP，过点A作直线BP的垂线交y轴于点Q．设点P的运动时间为t秒．
（1）求抛物线的解析式；
（2）当BQ=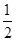AP时，求t的值；
（3）随着点P的运动，抛物线上是否存在一点M，使△MPQ为等边三角形？若存在，请直接写t的值及相应点M的坐标；若不存在，请说明理由．
，然后选择一个使分式有意义的数代入求值．
外一点，且BD=CD，
，点M，N分别在AB,AC上，若
,
的高DH，并证明DH=BD;
中，AD平分
且平分BC交BC于G，
于E,
交AC的延长线于F.
，求AE、BE的长.
中，AB=BC，
，D是AB上一点，AE⊥CD交其延长线于点E，且
,求D到AC的距离。
是
的算术平方根，
为
的立方根，求
的立方根；
粤公网安备 44130202000953号