（年福建福州14分）如图，抛物线
与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．
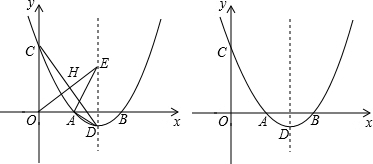
（1）求点A，B，D的坐标；
（2）连接CD，过原点O作OE⊥CD，垂足为H，OE与抛物线的对称轴交于点E，连接AE，AD．
求证：∠AEO=∠ADC；
（3）以（2）中的点E为圆心，1为半径画圆，在对称轴右侧的抛物线上有一动点P，过点P作⊙O的切线，切点为Q，当PQ的长最小时，求点P的坐标，并直接写出点Q的坐标．
相关试题
（年福建福州14分）如图，抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．
（1）求点A，B，D的坐标；
（2）连接CD，过原点O作OE⊥CD，垂足为H，OE与抛物线的对称轴交于点E，连接AE，AD．
求证：∠AEO=∠ADC；
（3）以（2）中的点E为圆心，1为半径画圆，在对称轴右侧的抛物线上有一动点P，过点P作⊙O的切线，切点为Q，当PQ的长最小时，求点P的坐标，并直接写出点Q的坐标．
，然后任选一个a的值代入求值.
粤公网安备 44130202000953号