(年湖南湘潭10分)△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC。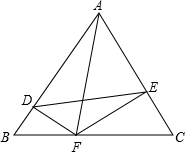
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值;
(3)已知A、D、F、E四点共圆,已知tan∠EDF=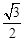 ,求此圆直径.
,求此圆直径.
(年湖南湘潭10分)△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC。
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值;
(3)已知A、D、F、E四点共圆,已知tan∠EDF=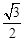 ,求此圆直径.
,求此圆直径.