（年福建厦门10分）如图，已知c＜0，抛物线y=x2+bx+c与x轴交于A（x1，0），B（x2，0）两点（x2＞x1），与y轴交于点C．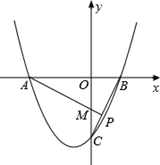
（1）若x2=1，BC=
，求函数y=x2+bx+c的最小值；
（2）过点A作AP⊥BC，垂足为P（点P在线段BC上），AP交y轴于点M．若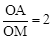
，求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式，并直接写出自变量的取值范围．
相关试题
（年福建厦门10分）如图，已知c＜0，抛物线y=x2+bx+c与x轴交于A（x1，0），B（x2，0）两点（x2＞x1），与y轴交于点C．
（1）若x2=1，BC=，求函数y=x2+bx+c的最小值；
（2）过点A作AP⊥BC，垂足为P（点P在线段BC上），AP交y轴于点M．若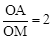，求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式，并直接写出自变量的取值范围．
-8
）÷4xy，其中x=2，y=1
-2
y+x
粤公网安备 44130202000953号