(本小题满分13分)如图,在四棱锥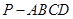 中,
中,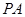 丄平面
丄平面 ,
,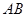 丄
丄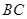 ,∠BCA
,∠BCA
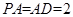 ,
,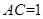 ,DC=
,DC=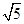
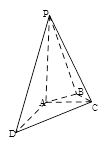
(Ⅰ)证明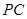 丄
丄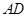 ;
;
(Ⅱ)求二面角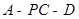 的正弦值;
的正弦值;
(Ⅲ)设E为棱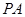 上的点,满足异面直线BE与CD所成的角为
上的点,满足异面直线BE与CD所成的角为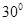 ,求AE的长.
,求AE的长.
相关知识点
推荐套卷
(本小题满分13分)如图,在四棱锥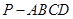 中,
中,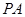 丄平面
丄平面 ,
,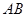 丄
丄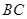 ,∠BCA
,∠BCA
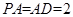 ,
,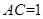 ,DC=
,DC=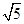
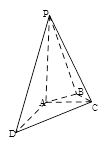
(Ⅰ)证明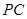 丄
丄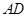 ;
;
(Ⅱ)求二面角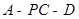 的正弦值;
的正弦值;
(Ⅲ)设E为棱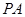 上的点,满足异面直线BE与CD所成的角为
上的点,满足异面直线BE与CD所成的角为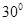 ,求AE的长.
,求AE的长.