如图,在矩形ABCD中,AB=6cm,BC=8cm.如果点E由点B出发沿BC方
向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为2cm/s和1cm/s.FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t(s)(0<t<4).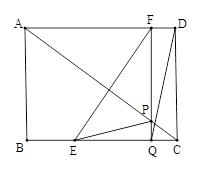
(1)连结EF、DQ,若四边形EQDF为平行四边形,求t的值;
(2)连结EP,设△EPC的面积为ycm2,求y与t的函数关系式,并求y的最大值;
(3)若△EPQ与△ADC相似,请直接写出t的值.
相关知识点
推荐套卷
 ;
; .
.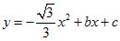 过A.B两点.
过A.B两点.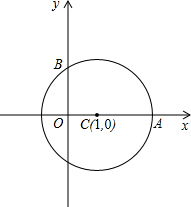

 ,点
,点 的坐标是
的坐标是 ,以点
,以点 为顶点的抛物线
为顶点的抛物线 经过
经过 轴上的点
轴上的点 .
.
 的坐标;
的坐标; 粤公网安备 44130202000953号
粤公网安备 44130202000953号