如图，在△ABC中，AB=BC，点E在边AB上，EF⊥AC于F．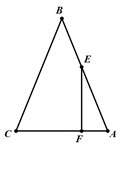
（1）尺规作图：过点A作AD⊥BC于点D（保留作图痕迹，不写作法）；
（2）求证：∠CAD=∠AEF；（3）若∠ABC=45°，AD与EF交于点G，求证：EG=2AF．
相关试题
相关知识点
推荐套卷
如图，在△ABC中，AB=BC，点E在边AB上，EF⊥AC于F．
（1）尺规作图：过点A作AD⊥BC于点D（保留作图痕迹，不写作法）；
（2）求证：∠CAD=∠AEF；（3）若∠ABC=45°，AD与EF交于点G，求证：EG=2AF．
粤公网安备 44130202000953号