（本小题满分10分）选修4-4：坐标系与参数方程
已知椭圆C：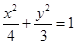
，直线
（t为参数）．
（Ⅰ）写出椭圆C的参数方程及直线
的普通方程；
（Ⅱ）设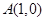
，若椭圆C上的点P满足到点A的距离与其到直线的距离相等，求点P的坐标．
相关试题
+
+
≥a+b+c.
,求a2+2b2+c2的最小值.
,n∈N+.
·
.相关知识点
推荐套卷
（本小题满分10分）选修4-4：坐标系与参数方程
已知椭圆C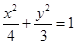：，直线（t为参数）．
（Ⅰ）写出椭圆C的参数方程及直线的普通方程；
（Ⅱ）设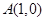，若椭圆C上的点P满足到点A的距离与其到直线的距离相等，求点P的坐标．
粤公网安备 44130202000953号