某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到 元.公司拟投入
元.公司拟投入 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
相关知识点
推荐套卷
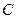 :
: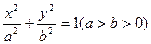 ,
, 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为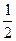 ,点
,点 在椭圆
在椭圆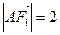 ,
,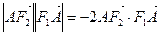 ,过
,过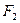 与坐标轴不垂直的直线
与坐标轴不垂直的直线 交椭圆于
交椭圆于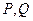 两点.
两点.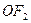 上是否存在点
上是否存在点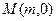 ,使得以线段
,使得以线段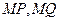 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数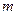 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.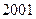 到
到 年十年间每年考入大学的人数.
年十年间每年考入大学的人数. 为方便计算,
为方便计算,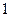 ,
, 年编号为
年编号为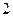 ,…,
,…, .数据如下:
.数据如下:
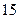 人的概率;
人的概率;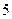 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出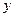 关于
关于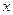 的回归方程
的回归方程 ,并计算第
,并计算第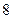 年的估计值和实际值之间的差的绝对值.
年的估计值和实际值之间的差的绝对值. ,底面三角形
,底面三角形 为正三角形,侧棱
为正三角形,侧棱
 底面
底面 ,
, 为
为 为
为 中点.
中点. 平面
平面 ;
;
 .
. 的单调递增区间;
的单调递增区间; 中,角
中,角 所对的边长分别为
所对的边长分别为 ,若
,若 ,
, ,求
,求 .
. 是实数,函数
是实数,函数 。
。 ,求
,求 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上的最大值。
上的最大值。 粤公网安备 44130202000953号
粤公网安备 44130202000953号