如图, 中,
中,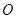 是
是 的中点,
的中点,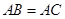 ,
,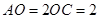 .将
.将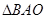 沿
沿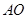 折起,使
折起,使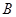 点与图中
点与图中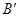 点重合.
点重合.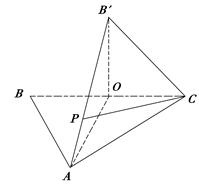
(Ⅰ)求证: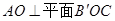 ;
;
(Ⅱ)当三棱锥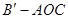 的体积取最大时,求二面角
的体积取最大时,求二面角 的余弦值;
的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试问在线段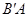 上是否存在一点
上是否存在一点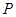 ,使
,使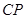 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ?证明你的结论.
?证明你的结论.
相关知识点
推荐套卷
如图, 中,
中,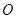 是
是 的中点,
的中点,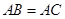 ,
,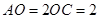 .将
.将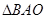 沿
沿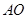 折起,使
折起,使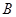 点与图中
点与图中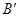 点重合.
点重合.
(Ⅰ)求证: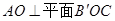 ;
;
(Ⅱ)当三棱锥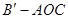 的体积取最大时,求二面角
的体积取最大时,求二面角 的余弦值;
的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试问在线段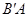 上是否存在一点
上是否存在一点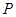 ,使
,使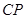 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ?证明你的结论.
?证明你的结论.