在某次考试中，从甲乙两个班各抽取10名学生的数学成绩进行统计分析，两个班成绩的茎叶图如图所示，成绩不小于90分的为及格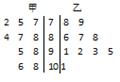
（1）用样本估计总体，请根据茎叶图对甲乙两个班级的成绩进行比较。
（2）求从甲班10名学生和乙班10名学生中各抽取一人，已知有人及格的条件下乙班同学不及格的概率；
（3）从甲班10人中抽取一人，乙班10人中抽取二人，三人中及格人数记为X，求X的分布列和期望。
相关试题
），且a⊥b．
)的值．
的最小正周期的最小值；
上的单调递减区间；
的最小正周期为
，且当
时，函数取最大值.
的解析式；
若△ABC的重心在
轴负半轴上，求实数
的取值范围．
＝（1＋
，1），
＝（1，
）（
，
∈R），且
的最小正周期；
的最大值是4，求
的图象经过怎样的变换而得到.推荐套卷
在某次考试中，从甲乙两个班各抽取10名学生的数学成绩进行统计分析，两个班成绩的茎叶图如图所示，成绩不小于90分的为及格
（1）用样本估计总体，请根据茎叶图对甲乙两个班级的成绩进行比较。
（2）求从甲班10名学生和乙班10名学生中各抽取一人，已知有人及格的条件下乙班同学不及格的概率；
（3）从甲班10人中抽取一人，乙班10人中抽取二人，三人中及格人数记为X，求X的分布列和期望。
粤公网安备 44130202000953号