（本小题满分13分）已知A（-2，0），B（2，0）为椭圆C的左、右顶点，F为其右焦点，P是椭圆C上异于A，B的动点，且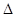
APB面积的最大值为2
．
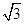（1）求椭圆C的方程及离心率；
（2）直线AP与椭圆在点B处的切线交于点D，当直线AP绕点A转动时，试判断以BD为直径的圆与直线PF的位置关系，并加以证明．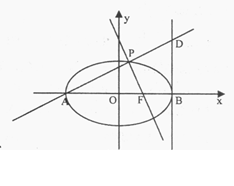
相关试题
的最小值.
且a+b+c=1，求证：
, 求mx+ny的最大值.
内接于圆
，
是圆
为平行四边形，
平面
，
，
。
求三棱锥
的体积
；
。
平面BCD；
推荐套卷
（本小题满分13分）已知A（-2，0），B（2，0）为椭圆C的左、右顶点，F为其右焦点，P是椭圆C上异于A，B的动点，且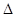APB面积的最大值为2．
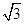（1）求椭圆C的方程及离心率；
（2）直线AP与椭圆在点B处的切线交于点D，当直线AP绕点A转动时，试判断以BD为直径的圆与直线PF的位置关系，并加以证明．
粤公网安备 44130202000953号